Two Port Networks

An electrical network with two separate ports for input and output.

Port

A pair of terminals through which current may enter or leave a network.

Parameters

Z parameters

Denoted by $[z]$. Aka. open-circuit impedance parameters. Measures impedance of the network. $$

$$\begin{bmatrix} V_1 \\ V_2 \end{bmatrix} = \begin{bmatrix} z_{11} & z_{12} \\ z_{21} & z_{22} \\ \end{bmatrix} \begin{bmatrix} I_1 \\ I_2 \end{bmatrix} = [z] \begin{bmatrix} I_1 \\ I_2 \end{bmatrix}$$

The parameters are found by setting $I_1$ and $I_2$ to $0$ in turn.

Y parameters

Denoted by $[y]$. Aka. short-circuit admittance parameters. Measures admittance of the network. $$

$$\begin{bmatrix} I_1 \\ I_2 \end{bmatrix} = \begin{bmatrix} y_{11} & y_{12} \\ y_{21} & y_{22} \\ \end{bmatrix} \begin{bmatrix} V_1 \\ V_2 \end{bmatrix} = [y] \begin{bmatrix} V_1 \\ V_2 \end{bmatrix}$$

The parameters are found by setting $V_1$ and $V_2$ to $0$ in turn. Same as the inverse of the $[z]$ parameters.

Transmission parameters

Denoted by $T$. Aka. ABCD parameters. Measures gain and transfer impedance and transfer admittance. $$

$$\begin{bmatrix} V_1 \\ I_1 \end{bmatrix} = \begin{bmatrix} A & B \\ C & D \\ \end{bmatrix} \begin{bmatrix} V_2 \\ -I_2 \end{bmatrix}$$

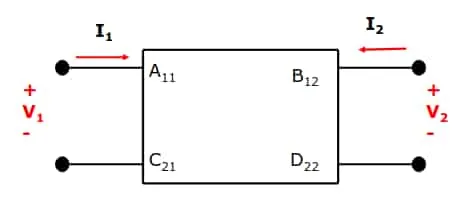
Here:

• $A$ - Voltage gain. Open circuit transfer function. Dimensionless.
• $B$ - Transfer impedance. Short circuit transfer impedance.
• $C$ - Transfer admittance. Open circuit transfer admittance.
• $D$ - Current gain. Short circuit current ratio. Dimensionless.

The parameters are found by setting $I_2$ and $V_2$ to $0$ in turn.

Reciprocal network

A network is said to be reciprocal if $AD-BC=1$. $$

Hybrid parameters

$$\begin{bmatrix} V_1 \\ I_2 \end{bmatrix} = \begin{bmatrix} h_{11} & h_{12} \\ h_{21} & h_{22} \\ \end{bmatrix} \begin{bmatrix} I_1 \\ V_2 \end{bmatrix} = [h] \begin{bmatrix} I_1 \\ V_2 \end{bmatrix}$$