Sahithyan's S2 — Theory of Electricity

Network Theorems

Definitions

Linear network

A network is linear iff frequency of the output signal is equal to the frequency of the input signal.

Thevenin’s theorem

Any linear electrical network containing only voltage sources, current sources and resistances can be replaced at terminals A-B by an equivalent combination of a voltage source $V_{th}$ in a series connection with a resistance $R_{th}$ .

$V_{th}=$ the voltage obtained at terminals A-B of the network with the terminals A-B open circuited.
$R_{th}=$ the resistance that the circuit between A-B terminals would have if all the current and voltage sources are set to to provide 0 currents or voltages.

Norton’s theorem

In a network made of linear time-invariant resistances, voltage sources and current sources, at a pair of terminals, it can be replaced by a current source and a resistor connected in parallel.

In AC circuits, this theorem can be applied to reactive elements as well.

$I_{no}=$ the current flowing between the terminals as the terminals are short circuited
$R_{no}=\frac{V_{no}}{I_{no}}$ where $V_{no}$ is the voltage between the terminals with no load

Superstition theorem

In a linear network with several independent sources, any voltage or current in the circuit can be found as the algebraic sum of the corresponding values obtained by assuming only one source at a time, with all the other sources turned off.

Reciprocity theorem

In a reciprocal network, if an emf $E$ in one branch produces a current $I$ in another, then if the emf $E$ is moved to the second branch, it will cause the same current in the first branch, where the emf has been replaced by a short circuit.

Compensation theorem

In a linear, bilateral network, any element can be replaced by a voltage source of magnitude equal to the current passing through the element multiplied by the value of the element.

Bilateral network

A circuit whose characteristics are the same when the direction of current through various elements. In a linear passive bilateral network, an excitation and its response can be interchanged.

Maximum Power Transfer theorem

Aka. Jacobi’s law. The theorem states how to choose (so as to maximize power transfer) the load resistance, once the source resistance is given. It does not say how to choose the source resistance for a given load resistance. The source resistance that maximizes power transfer from a voltage source is always $0$ (the hypothetical ideal voltage source).

In a purely resistive network, the load resistance must be equal to the load resistance.

R_L = R_S \quad \text{and}\quad P_\text{max} = \frac{E^2}{4R_L}

In an AC network, the load impedance must be equal to the conjugate of the load impedance.

Z_L = \bar{Z_S} \quad \text{and}\quad P_\text{max} = \frac{E^2}{4R_S}

And if the load power factor is fixed, the magnitudes of the load impedance and the source impedance must be equal.

|Z_L| = |Z_S| \quad \text{and}\quad P_\text{max} = \frac{E^2}{4R_S}

In an AC network, if the load is a resistive load and the source has a complex impedance, the load resistance must be equal to the magnitude value of the source impedance.

R_L = |Z_S| \quad \text{and}\quad P_\text{max} = \frac{E^2 |Z_S|}{2 |Z_S|(R_S+|Z_S|)}

Millmann’s theorem

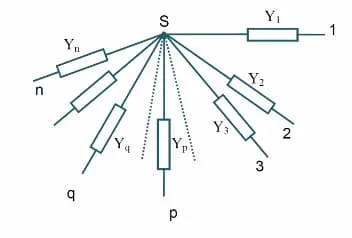
Millmann's theorem

Suppose there are $n$ number of admittances which share a point $S$ and the other ends are open.

V_{\text{SN}} = \frac {\sum_{p=1}^n {Y_\text{P} V_{\text{PN}}}} {\sum_{p=1}^n {Y_\text{P}}}

Equivalent Generator theorem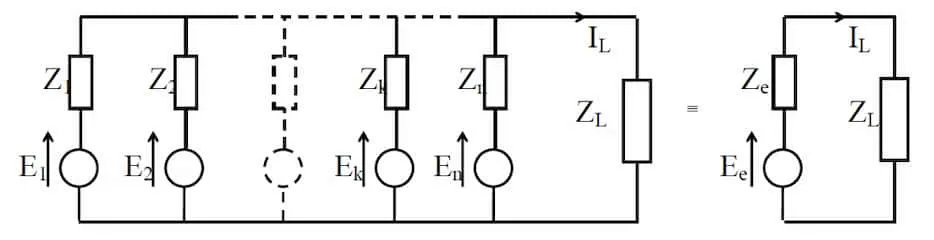

An extension of Millmann’s theorem. A system of voltage sources operating in parallel may be replaced by a single voltage source in series with an equivalent impedance. This is also Thevenin’s theorem applied to generators in parallel.

E_\text{eq}= \frac {1} {Y_\text{eq}} {\sum_{k=1}^n E_k Y_k}

Y_\text{eq}= {\sum_{k=1}^n Y_k}

Rosen’s theorem

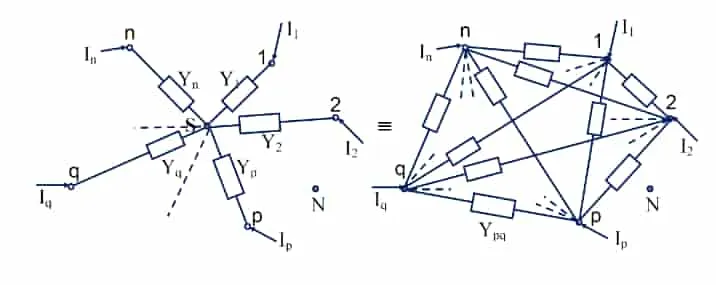
Rosen's theorem

Used to convert star connected network to mesh equivalent. External conditions will not be affected.

Y_{\text{pq}} = \frac{Y_p Y_q}{\sum_{k=1}^n Y_k}

When $n=3$ , the conversion becomes quite simple.

Delta to Star

R_{\text{A}} = \frac{R_\text{AB} \times R_\text{AC}}{R_\text{AB} + R_\text{BC} + R_\text{AC}}

$R_\text{B}, R_\text{C}$ can be found similarily.

Star to Delta

Y_{\text{AB}} = \frac{Y_\text{A} \times Y_\text{B}}{Y_\text{A} + Y_\text{B} + Y_\text{C}}

$Y_\text{BC}, Y_\text{AC}$ can be found similarily.