Coupled Circuits

For all the definitions below, $N$ means the number of turns. $$

Self inductance

When the magnetic field produced by a coil causes an emf on itself. Denoted by $L$. Measured in henry ($H$).

For a coil having $L_p$ self inductance, $N$ turns, carrying current $i_p$, the generated $\phi_p$ is given by:

$$L_p = \frac{N_p \phi_p}{i_p} = \frac{N_p^2 \mu A}{l}$$

Mutual coupling

Mutual coupling between coils exist when one (secondary coil) is in the magnetic field created by the other coil (primary coil).

When a time-varying current $i_p$ flows in the primary coil, a time-varying flux $\phi_p$ is produced, which produces a back emf $e_p$.

Magnetic field

Magnetic flux density

Measure of strength and direction of the magnetic field. Denoted by $B$. Measured in tesla ($T$) or $kgs^{-2}A^{-1}$ or $Nm^{-1}A^{-1}$.

Magnetic flux

Denoted by $\phi$. Measured in weber ($\text{Wb}$).

$$\phi = \int B\,\text{d}A = BA$$

Magnetic field strength

Aka. magnetic field intensity. Denoted by $H$. Measured in ampere per meter ($Am^{-1}$).

Magnetic permeability

Measure of magnetization on a material when a magnetic field is applied. Depends on the material. Denoted by $\mu$. Measured in $Hm^{-1}$ or $NA^{-2}$.

Note

Relationship between magnetic flux, permeability, and intensity.

$$B = \mu H$$

Flux linkage

Denoted by $\lambda$. Defines the interaction of a multi-turn inductor with a magnetic flux. $$

$$\lambda = N\phi$$

Magnetomotive force

A force acted on a coil carrying current. Denoted by $\text{mmf}$. $$

$$\mathfrak{f} = Ni$$

Here:

• $N$ - number of turns
• $i$ - current in the coil

It’s similar to electromotive force in electrical circuits.

Reluctance

Reluctance of a path for magnetic flux:

$$\mathcal{R} = \frac{l}{\mu A} = \frac{\mathfrak{f}}{\phi}$$

Here:

• $l$ - Length of the path
• $\mu$ - Permeability
• $A$ - Cross-sectional area

The above equation can be thought of the equation of resistance in electrical context. $1/\mu$ is used instead of $\rho$.

$f=\mathcal{R}\phi$ is similar to $V=IR$ in electrical context.

Note

For a toroidal core having $R$ radius and $2r$ thickess:

$$\mathcal{R} = \frac{2R}{\mu r^2}$$

Fringing

Flux lines in the air gap tend to bow out. Thus the effective area of air gap is larger than the cross sectional area of the core.

$$A_\text{gap} = (\text{width} + \text{gap length}) \times (\text{thickness} + \text{gap length})$$

Laws

Faraday’s Law

The magnetic flux passing through a surface $A$ is given by the surface integral: $$

$$\phi = \int {B\cdot \text{d}A} = BA$$

Ampere’s Law

Line integral of magnetic field intensity around a closed path is equal to the sum of the currents owing through the surface bounded by the path.

$$\oint H \cdot \text{d}l = \sum i$$

When $H$ is constant (magnitude and direction) along the path, the above equation reduces to $Hl = \sum i$.

When $H$ is constant and the path has $N$ turns, $Hl = Ni$.

Mutual inductance

When 2 coils are coupled, part of the magnetic flux produced in the primary coil links with secondary coil.

Coefficient of coupling

Ratio between the produced magnetic flux and linked magnetic flux. Denoted by $k\;(\le 1)$. $$

$$\phi_s = k\phi_p$$

Induced emf

Since the produced flux is time-varying, an emf $e_s$ is induced in the second coil. $$

$$e_p = N_p \frac{\text{d}\phi_p}{\text{d}t}$$ $$e_s = N_s \frac{\text{d}\phi_s}{\text{d}t}$$

In the linear region of magnetization characteristic:

$$\phi_p \propto i_p \implies e_s = \frac{N_s \phi_m}{i_p}\frac{\text{d}i_p}{\text{d}t} = M_{SP} \frac{\text{d}i_p}{\text{d}t}$$

Here $M_{SP}$ is the mutual inductance. $$

$$M_{SP} = \frac{N_s \phi_s}{i_p} = \frac{k_{SP}N_sN_p\mu A}{l}$$

Practically, coupling between the primary and secondary coils is identical to the coupling between secondary and primary coils.

$$k_{SP} = k_{PS}$$ $$M_{SP} = M_{PS}= M= k\sqrt{L_pL_s}$$

Energy stored

$$\text{Total stored energy}= \int{v_pi_p\text{d}t}+ \int{v_si_s\text{d}t}$$ $$\text{Total stored energy}= \frac{1}{2}L_pi_p^2+ \frac{1}{2}L_si_s^2 \mp Mi_pi_s$$

The last component is the effective energy stored in the mutual inductance.

The mutual inductance energy is:

• Added; if produced fluxes aid each other
• Subtracted; if produced fluxes oppose each other

Equivalent inductance

In series

$$L_\text{eq} = L_1 + L_2 \pm 2M$$

The mutual inductance is:

• Added; if produced fluxes aid each other
• Subtracted; if produced fluxes oppose each other

In parallel

$$L_\text{eq} = \frac{L_1 L_2 - M^2}{L_1 + L_2 \mp 2M}$$

The mutual inductance in the denominator is:

• Subtracted; if produced fluxes aid each other
• Added; if produced fluxes oppose each other

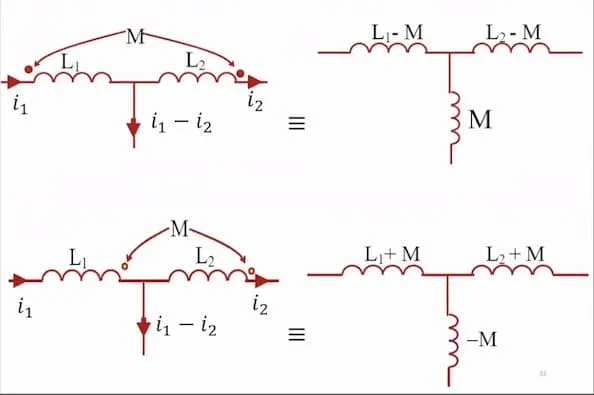
T-junction

If 2 coils are given in a T-junction, the circuit has to be changed to include a 3rd inductor. If the coils were aiding, the 3rd inductor will be $-M$, otherwise $M$. The 3rd inductor value will be subtracted from the other 2 inductors.

Dot notation

One terminal of the coils is marked with a dot. If both currents enter or exit from the dotted terminals, the fields aid; mutual inductance is positive. Otherwise the fields oppose; mutual inductance is negative.

Note

When a single coil is considered, the induced voltage would oppose the applied voltage or the current flow.