Adders

Half Adder

A digital circuit component that adds 2 bits. Outputs 2 bits: sum bit and carry bit.

$$S = A \oplus B \;\; \text{ and } \;\; C = A \cdot B$$

Full Adder

A digital circuit component that adds 3 bits. Outputs 2 bits: sum bit and carry bit. An extension of the half adder where the carry bit of a half adder is input to another half adder. Built using 2 half adders.

$$S = \overline{A}\cdot \overline{B} C_\text{in} + \overline{A} {B} \overline{C_\text{in}} + {A} \overline{B}\cdot \overline{C_\text{in}} + {A} B C_\text{in}$$ $$C_\text{out} = \overline{A} B C_\text{in} + A B + A\overline{B}C_\text{in}$$

Ripple Carry Adder

Made by a chain of full adders joined as mentioned below:

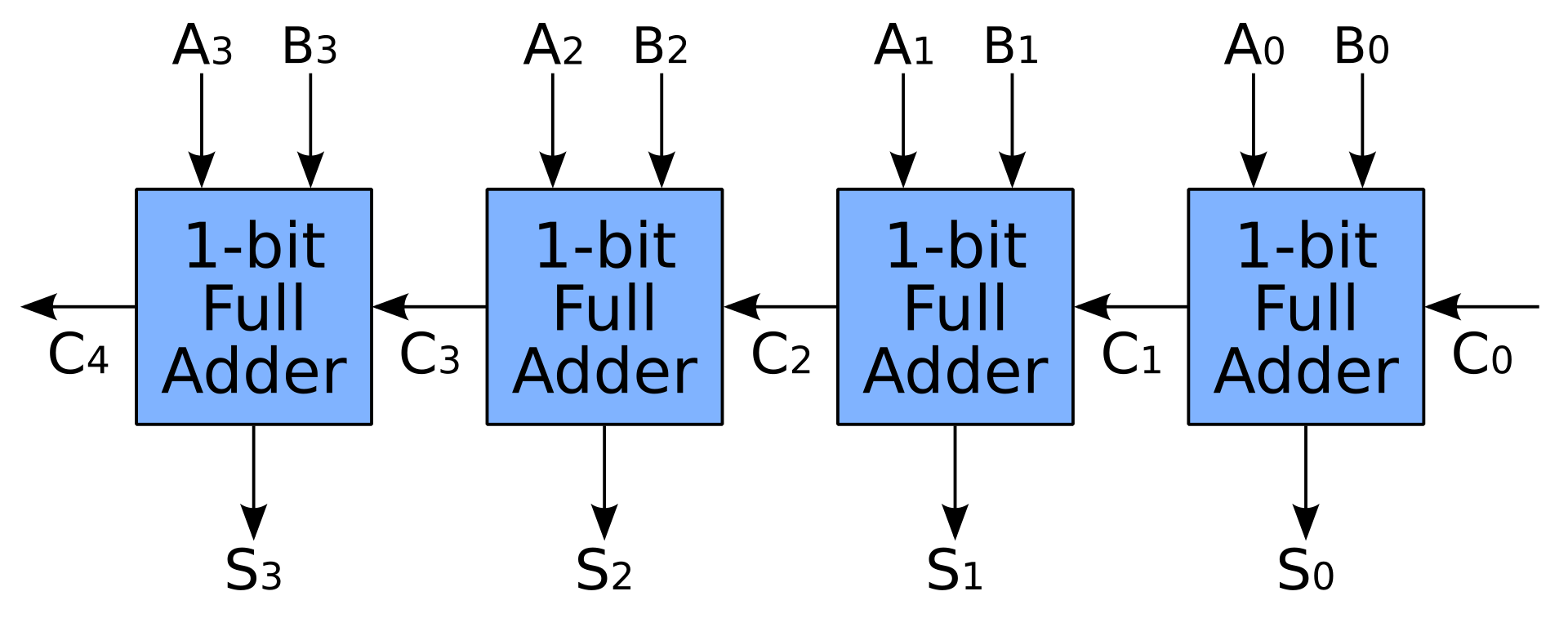
Image from Wikipedia.

Carry output of each FA ripples forward to calculate the output. Delay increases with number of bits.

Carry Lookahead Adder

A technique to speedup binary addition by calculating carry bits in parallel. In a CLA:

• Carry generate - means C_out will be created
• Carry propogate - means C_in will be sent out as C_out

$$P_i = A_i \oplus B_i \;\;\;\; G_i = A_i B_i$$ $$S_i = P_i \oplus C_i \;\;\;\; C_{i+1} = G_i + P_i C_i$$

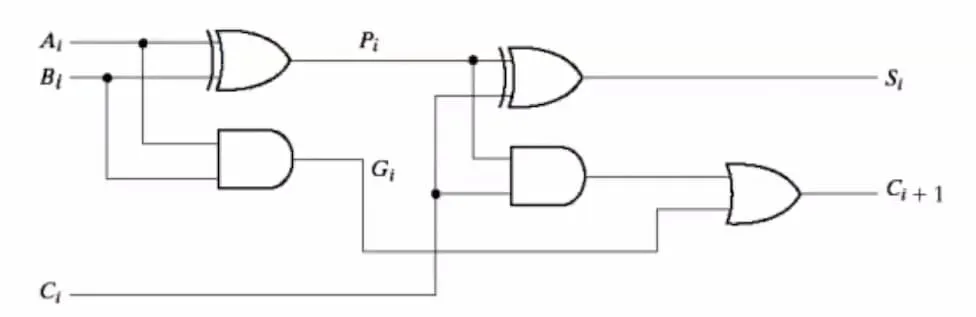
The CLA can be used to create n-bit adders which only have 3 level delay. Faster than RCA.

3 levels of delay:

• Generate & propagate signals
• Carry lookahead (sum-of-products)